무냐의 개발일지
[3/12] 컴퓨터비전2_ CNN(Convolutional Neural Network) 본문
- 딥러닝을 이용한 이미지 분석의 핵심은 Convolution 연산을 통해서 이미지의 숨겨진 패턴을 찾는 자동 패턴 추출기인 filter를 학습시키는 것입니다.
(요게 진짜 CNN에 대한 완벽한 설명임!)
1. CNN
- 이미지 데이터는 3개의 채널을 갖고 있지만, 일단은 채널 1개일 때 Convolution 연산이 어떻게 일어나나 보자

Convolution + Pooling 을 거듭한다 -> 1-Dimensional vector 만드는 Flatten -> MLP 구조 (Fully connected) -> Output
* CNN 구조는 크게 Feature extraction과 Classification으로 구성됩니다.
- Input이 들어가면 먼저 Convolution 연산과 Pooling을 여러 번 반복하여 Feature extraction을 한 후
- 1D 데이터인 flatten layer로 만듭니다. (flatten하면서 위치정보가 사라진다)
- 마지막으로 Fully connected layer(MLP)를 통해 classification을 합니다.
| Convolution 연산
- Convolution 연산은 Input에 kernel을 over-riding하여 겹쳐지는 숫자를 곱하여 그 값을 더하는 것입니다.
- stride를 1로 지정하여 Convolution 연산을 반복하면 feature map이 나옵니다.
예)


Input (7x7) 데이터 & Kernel (3x3) (특징 추출기) 이 있다.
Kernal을 Input 이미지 (original image data)에 올린다 : over-riding
over-riding 해서 겹쳐지고, 각각 곱해주고, 더해주면, 하나의 값이 나온다. -> stride= 1 (kernel을 몇 칸 이동시킬 것인가)


이런 식으로 커널을 오른쪽으로 1칸 이동해서, 똑같이 곱해준 값을 더해서, 하나의 값을 낸다
끝까지 반복 -> 한 칸 아래로 내려와서, 왼쪽부터 반복 -> 마지막까지 간다 -> convolution stop

연산 종류 후 남은 것 : feature map
(참고 자료)
Image Kernels explained visually
An image kernel is a small matrix used to apply effects like the ones you might find in Photoshop or Gimp, such as blurring, sharpening, outlining or embossing. They're also used in machine learning for 'feature extraction', a technique for determining the
setosa.io
They're also used in machine learning for 'feature extraction', a technique for determining the most important portions of an image. In this context the process is referred to more generally as "convolution"
2. Filter (kernel과 거의 동의어로 쓰이지만 다르다)
: filter는 feature extractor입니다. 이미지 데이터가 가지고 있는 특징, pattern을 추출해 주는 역할을 합니다. filter가 많을수록 여러 개의 feature map이 생기며 복잡하고 다양한 pattern을 찾을 수 있습니다.
| Hand-crafted filter (Hand-crafted Feature)

- 일일이 수작업으로 필터를 찾으려고 했음.
- 필터를 많이 확보하는게 핵심 경쟁력였기 때문에 이걸 한땀 한땀 만들었음.
- 사진이 흐리고 정보가 불분명할 때, 이미지의 정보성, 특징, 패턴이 두드러지게 확인될 수 있도록 하는 Filter
- MLP에서는 hidden layer들이 feature extraction 역할을 한다.
한계점) 사람이 직접 찾아야 했다는 점 -> 개선) Deep learning 구조를 통해 filter를 자동으로 만들 것이다 (CNN은 커널, 필터를 다양하게 만듦으로써 이미지의 특징을 잘 뽑아내도록 할 것이다)
3. Padding (feature map 사이즈 증가시켜서 계속 convolution 연산 할 수 있도록 한다)
layer가 여러개일때는?
convolution 연산을 거듭할수룩 7x7 -> 5x5 -> 3x3 -> 1x1 총 레이어가 3개 더 생긴다. 하지만 feature map 사이즈가 작아져서, 더 이상 연산을 수행할 수 없게된다.
그래서 padding이 등장했다.

- Filter 적용 전, 보존하려는 feature map 크기에 맞게, Feature map 좌우상하끝에 각각 열, 행을 추가한다 (회색)
- 여기에 0 값을 채워서, feature map 사이즈를 증가시킨다. (웬만하면 대부분의 경우 0값을 넣는다)
- Stride 수, padding 값을 어떻게 설정할 것인지 추구 학습
1. Channel이 3개일때 (channel = R,G,B)

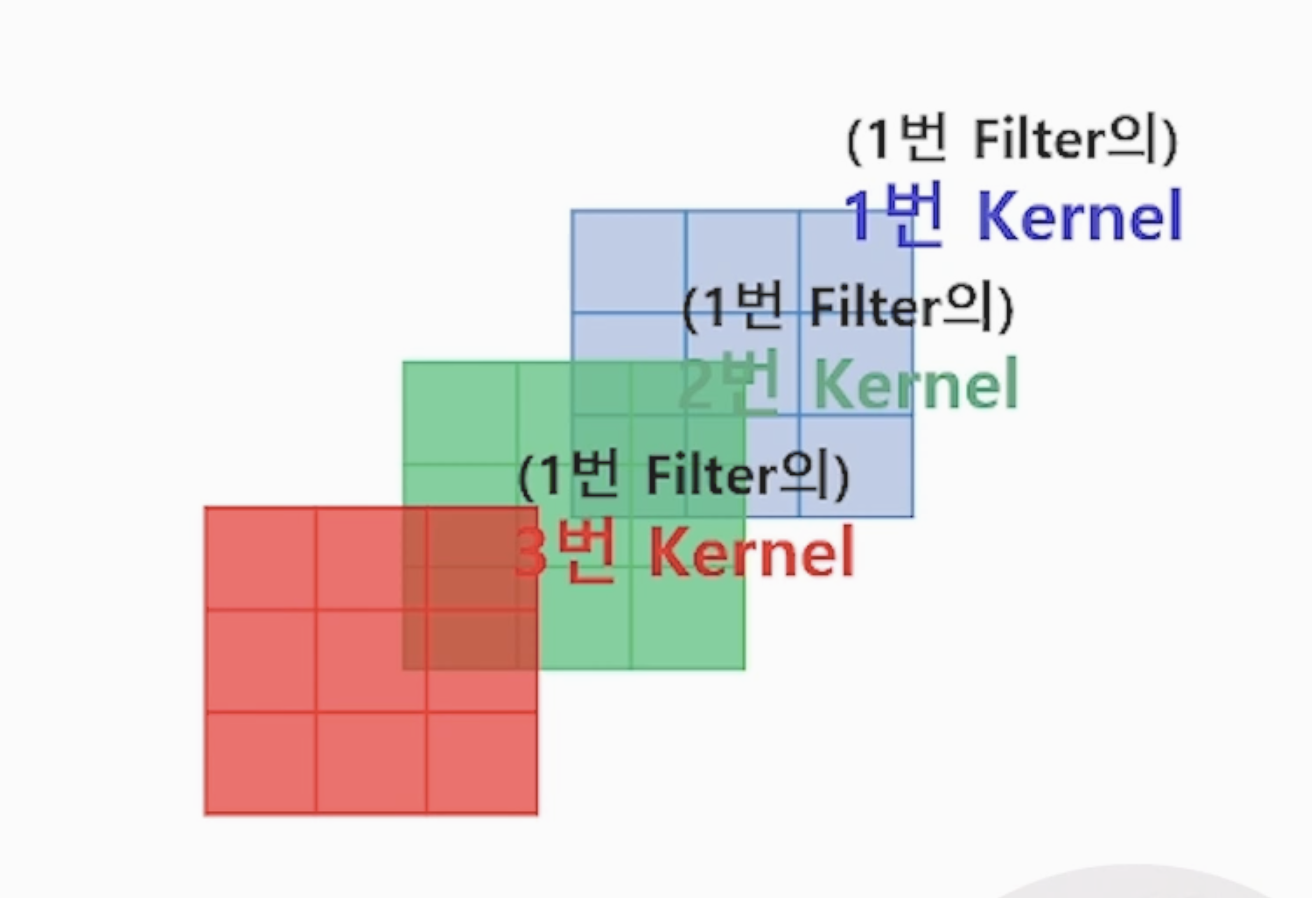
- 채널이 R,G,B 3개고, 그에 맞는 커널이 각각 하나씩 붙게 된다.
- 커널과 필터는 비슷하지만 같지는 않다. 필터가 가장 상위 개념임. (커널은 존재하는 채널 갯수만큼 존재한다). 커널 3개 = 필터
순서는 똑같다. overriding을 각각의 채널에 시행해준다


stride = 1, input = 7x7, output = 5x5 (3개), kernel= 3x3
나온 feature map들에 bias 값을 더해준다.

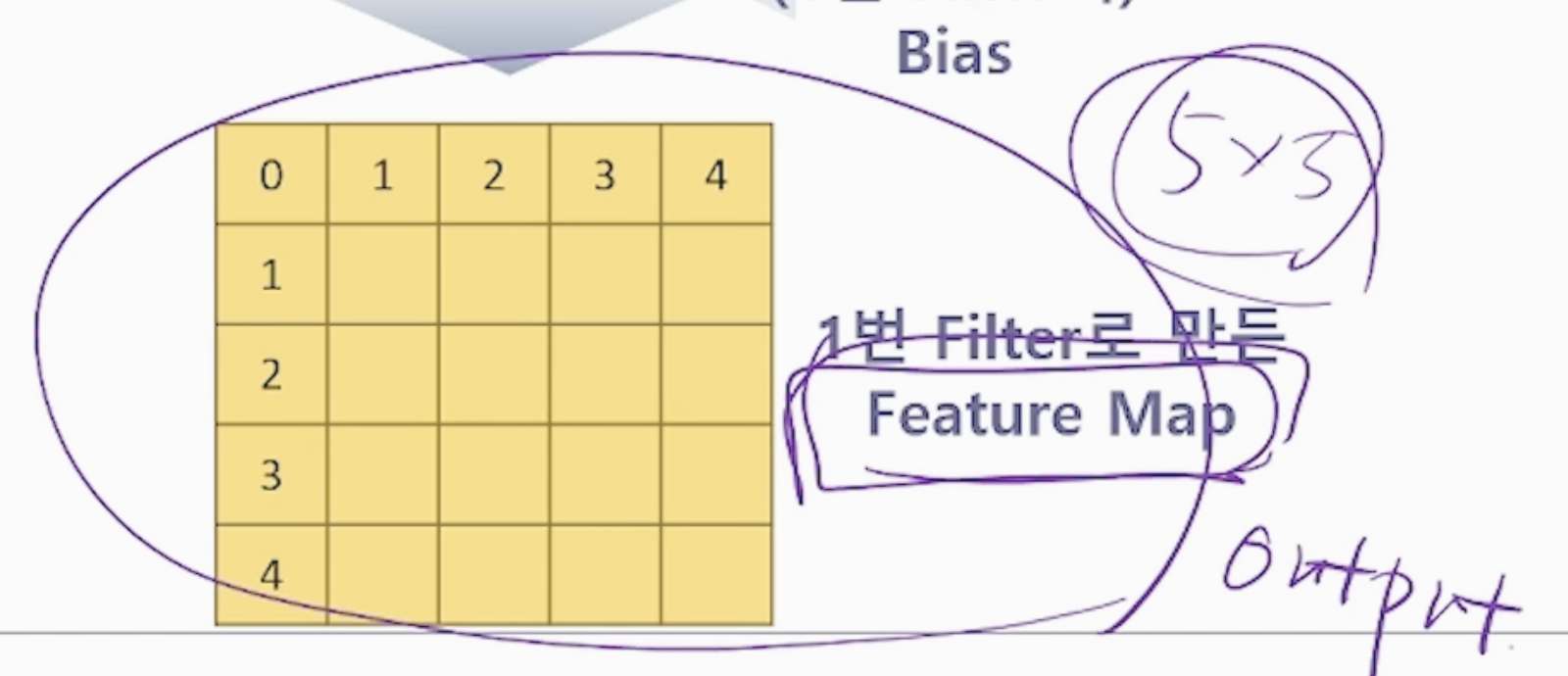
- 최종적으로 bias를 추가해서 더해준 값이 최종 feature map
- filter 하나로 feature map (= activation map) 하나가 나왔다
- filter (=feature extractor) 의 갯수가 feature map의 갯수를 결정한다
- input의 채널수는 feature map의 채널 수와 같지 않다
7x7x3 -> 5x5x2(feature map의 최종 갯수)
- kernel은 input의 channel 수만큼 존재하고,
- 각 channel 수준에서 Convolution 2D 연산을 계속하면 channel 수만큼의 output이 생깁니다.
2. Hyper Parameter (kernel size, channel size, stride등)
Kernel Size
- Kernel size가 커질수록 연산을 통해 찾아야 하는 파라미터의 수가 증가하게 됩니다.
- Kernel size가 작아질수록 데이터에 존재하는 global feature보다 local feature에 집중하게 됩니다. 쉽게 표현하자면 큼직한 특징보다는 지엽적인 특징에 집중해서 패턴을 찾게 됩니다.
Channel size
- Filter의 channel size가 커질수록 convolution 연산을 통해서 더 다양한 패턴을 찾을 수 있습니다.
- 그러나 channel의 사이즈가 커짐에 따라서 연산으로 찾아야 하는 파라미터의 숫자가 증가하게 됩니다.
Stride
- Stride 값이 커지면 데이터를 빠르게 훑고 지나가는 연산을 하게 됩니다.
- 따라서 지역적인 특징을 꼼꼼하게 살펴보아야 할 경우에는 stride값을 크게 하는 것이 좋지 않습니다.
안타깝게도 이러한 hyperparameter의 값을 어떻게 정하는 것이 최적이라는 규칙을 찾는 것은 매우 어려운 일입니다. 따라서 연구자는 시행착오를 스스로의 실습으로 해거나 AutoML과 같은 방법으로 hyperparameter를 스스로 tuning해야 합니다.
AutoML은 머신러닝과 딥러닝을 적용할 때마다 반복적인 과정으로 발생하는 비효율적인 작업(하이퍼 파라미터 실험, 문제 적합한 architecture를 찾는 과정 등)을 최대한 자동화하여 생산성과 효율을 높이기 위하여 등장한 것으로, 현재 다양한 툴들이 개발되어 있습니다.
• 파라미터 (Parameter) : 파라미터는 모델 내부에서 학습되는 변수입니다. 모델 학습과정에서 업데이트 됩니다.
예) weight coefficient(가중치 계수), bias(편향치)
• 하이퍼파라미터 (Hyperparameter) : 하이퍼 파라미터는 사용자가 직접 세팅해 주는 값을 말합니다. 학습과정 동안 변경되지 않습니다.
예) learning rate, batch size, regularization파라미터, epoch 등
(참고) 1x1 Convolution
Convolution 학습을 수행하는 layer를 사용해서 원하는 모델을 구성할 때는 Filter의 Channel 수를 직접 결정해야 합니다. 이전에 언급한 대로, 일반적으로는 좋은 성능을 보이는 논문에서의 구조를 그대로 따라하지만, 때로는 연구자가 직접 결정해주어야 합니다.
channel size가 지나치게 크면 학습을 통해 찾아야 하는 파라미터 숫자가 증가하기 때문에 많은 연산 비용을 들여야만 합니다.
하지만 1x1 Convolution을 사용하면 연산량을 매우 쉽게 줄일 수 있습니다.
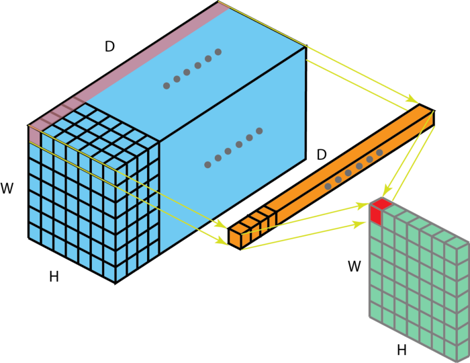
때로는 feature map의 가로 세로 사이즈는 변화시키지 않고 channel size만 변형하고 싶을 때가 있습니다.
물론 padding을 통하여 가로 세로 사이즈에 대한 변경없이 channel size만 변경할 수 있지만, 파라미터 숫자 증가에 따른 연산량 증가의 문제를 피할 수 없습니다.
이럴 때 1x1 convolution은 연산량의 문제를 회피하면서도 channel size를 원하는 대로 변경하는 데에 도움을 줍니다.
[예시 1] 28x28x192 image 데이터에 (5x5 filter, 32 channel) convolution 연산을 적용한다고 해 봅시다. 이때, feature map의 크기와 파라미터 수에 대해서 생각해 보세요.
예시 1의 feature map의 크기는 24x24x32가 나옵니다. 파라미터 수(연산량) 는 28 x 28 x 32 x 5 x 5 x 192 = 120,422,400 약 1.2억 번의 연산이 필요합니다.
[예시 2] 28x28x192 image 데이터에 (1x1 filter, 16 channel) convolution 연산을 사용하여 channel을 줄인 뒤, 이어서 (5x5 filter, 32 channel) convolution 연산을 적용 한다고 해 봅시다. 이때, feature map의 크기와 파라미터 수에 대해서 생각해 보세요.
예시 2의 feature map의 크기도 24x24x32가 나옵니다.
먼저, 1x1 filter를 사용해서 크기를 줄일 때 사용되는 파라미터 수(연산량)는 28 x 28 x 16 x 1 x 1 x 192 = 2,408,448 약 240만 번의 연산이 필요합니다. 다시 5x5 filter를 사용하면 28 x 28 x 32 x 5 x 5 x 16 = 10,035,200 약 1000만 번의 연산이 필요합니다. 그럼 총 약 1240만 번의 연산이 필요합니다.
예시 1과 예시 2의 파라미터 수(연산량)는 1.2억 번(12000만 번) 과 1240만 번의 연산으로 10배 가까이 차이 나는 것을 확인할 수 있습니다. 실제로 1x1 convolution은 연산량의 문제를 회피하면서도 channel size를 원하는 대로 변경하는 데에 도움을 줍니다. 직접 수치로 비교하니 더 이해가 잘 되지 않나요? 🤔😉
3. Transposed Convolution (= Up-convolution , Deconvolution, Up-sampling)
: 네트워크에서 업샘플링을 수행하고 고해상도의 특징 맵을 생성하는 데 사용됩니다.
: 더 큰 이미지로 확대, 고해상도의 정보를 복원/복구 등의 특징이 있다.
: Auto-Encoder 구조에서 입력 정보가 압축된 compressed representation을 다시 원래 입력 사이즈로 반환하기 위해 사용합니다. 정보를 축약하는 down-sampling이라는 표현과 반대로 up-sampling 한다고 말하기도 합니다. Low-resolution의 이미지를 high-resolution으로 바꾸는 역할도 할 수 있고, Pixel 별로 할당된 정답 값을 맞추는 task인 semantic segmentation에서도 활용할 수 있습니다.
- 줄어들었던 걸 다시 펴주는 과정

압축 -> latent (은닉, 보이지 않는) 보이지 않는 패턴을 찾아낸 결과 0> 압축 해제
앞에서는 convolution 연산을 해서 자동으로 사이즈가 줄어든다 (채널도 줄어들고) -> 압축을 해제하는 게 Transposed Convolution
Encoder - Decoder 구조
down-sampling - up-sampling
- low resolution image 를 high resolution image로 바꿀 때 사용한다
- pixel 별로 할당된 정답값을 맞추는 task인 Semantic Segmentation에서도 활용할 수 있다 (segmentation 전반에서 다 활용된다)

1. Pooling (끄집어 낸다) : 연산량을 크게 늘리지 않으면서 줄이고 싶을 때
: Feature map으로 표현된 정보를 축약한다
: parameter 값을 곱하거나 더하는 등 사용 없이, 정보를 압축할 수 있다는 장점이 있다 (파라미터가 아예 필요 없다. 심플!)
: 비선형성을 강화하고, 연산성능을 향상시킨다
: 지나치게 디테일한 정보는 추려내고, 가장 중요한 정보들만 뽑아낼 수 있다
- Max pooling : 가장 큰 값만 뽑아낸다 - 가장 두드러지는 특징만 남기는 효과
- Average pooling : 평균치를 뽑아낸다 - 영상의 일반적인 양상을 남기고, 노이즈를 줄여주는 효과를 기대한다


Input - Conv - Pool 반복 - Fully connected Layer(MLP) - Classification 하는 softmax

2. Convolution + Pooling

- CNN의 깊이를 증가시키는 게 매우 중요하다!
- CNN은 크게 Feature Extraction과 Classification 영역으로 구성됩니다. 연속적인 CNN 연산(Convolution + Pooling)을 순차적으로 수행하면서 일련의 Feature Map을 생성합니다. CNN 연산을 통해 순차적으로 생성된 Feature map의 크기(높이x너비)는 줄어들지만 채널(깊이)은 증가합니다.
3. CNN 구조
'Data Scientist Bootcamp' 카테고리의 다른 글
| [3/14] 컴퓨터비전4 _Object detection, Segmentation (2) | 2024.03.14 |
|---|---|
| [3/13] 컴퓨터비전3 _ 심화 CNN, Transfer Learning (0) | 2024.03.13 |
| [3/11] 컴퓨터비전1 (0) | 2024.03.11 |
| [3/8] 딥러닝 심화3 (가중치 초기화, 배치정규화) (2) | 2024.03.08 |
| [3/8] 딥러닝 심화2 (모델의 과소적합, 과대적합을 방지하기 위한 방법 3가지) (0) | 2024.03.08 |




