무냐의 개발일지
[3/7] 딥러닝 기초 (퍼셉트론, 인공신경망) 본문
1. 인공신경망
* 인공신경망(artificial neural network) : 인간 뇌 구조, 그 중에서도 뉴런- 뉴런 사이 전기신호를 통해 정보 전달하는 것에서 아이디어 얻음. 신경 세포의 구조와 동작을 모방. input, output
* 뉴런(신경세포) : 수상돌기(다른 신경세포의 축색돌기와 연결되어 신호를 받아들임), 축색돌기(특정 값 이상이면 신호를 내보낸다), 신경연접(시냅스: 전달되는 신호 증폭)
* 인공 뉴런 : node, edge로 구성되어 있고, 하나의 node 안에서 input, weights 를 곱하고 더하는 linear 구조이며, activation function 을 통해 non-linear 표현도 가능하다 (relu같은)
* 인공신경망 구조 : 인공 뉴런들이 여러개 모여서 연결된 형태 (input, hidden, output layer)

2 .인공신경망 역사

퍼셉트론 : 스스로 학습하는 인공신경망 등장 (1957)
딥러닝 이라는 용어 등장 (2006)
딥러닝 이후 빠르게 발전했다.
*최초의 인공 신경망 : 인간 신경계를 활성/비활성 2개로만 나타내는 이진 뉴런으로 표현 (흥분/억제 상태이냐에 따라만 신호가 전달되고, 임계치가 넘어야만 신호가 나오는 것)
*퍼셉트론(perceptron) : 인공 신경망이 스스로 문제에 맞춰 학습한다. 입력값, 가중치, 활성화함수로 이뤄진 간단한 구조이다. 원하는 출력값을 내보내도록 가중치를 조정해가는 작업이 '훈련, 학습'이다. 다만, 단순 퍼셉트론은 비선형 문제를 해결할 수 없다.
(예를 들어, XOR 게이트는 단일 퍼셉트론으로는 해결할 수 없는 문제다. XOR 게이트는 두 입력이 서로 다를 때만 출력이 1이 되는 논리 연산을 수행하는데, 단일 퍼셉트론은 선형 경계를 가지기 때문에 XOR 게이트와 같은 비선형 문제를 해결할 수 없다.)
따라서 XOR 게이트




* 다층 퍼셉트론(Multi- layer perceptron) 을 써야만 이런 문제를 해결할 수 있다. 그래서, 인공신경망은 다층 퍼셉트론 구조로 이뤄져있다. 여러개의 퍼셉트론을 층으로 구성한 신경망 모델이다. 다만, 다층 퍼셉트론은 학습이 어려워. 왜냐면, 활성화함수가 계단 함수인데, 많은 은닉층의 수와 미분이 불가능한 계단함수의 존재가 학습의 난이도를 높인다. 학습을 하려면 미분 가능한 함수가 필요하다.


* 역전파 알고리즘 :
- 순전파(forward propagation) : 신경망에서 입력값 -> 입력층, 은닉측, 출력층 도달까지의 계산 과정. 층을 통과할 때마다 입력값에 가중치를 곱해 다음 층으로 출력할 값을 계산
- 역전파(back propagation) : 순전파로 입력값으로부터 출력값 계산 -> 이 순전파로 구한 출력값 & 실제 target값 차이(손실) 구함 -> 손실 줄이는 방향으로 가중치의 기울기 구함(경사하강법) -> 기울기를 바탕으로 가중치 갱신하며, 이때 출력층 -> 입력층 방향으로 차례로 가중치 갱신(역전파) -> 이 갱신된 가중치를 바탕으로 위 단계를 계속 반복하여 손실값을 줄여나간다.
3. 딥러닝 역사
* 일반 인공신경망 : 은닉층이 소수. 특징을 일일이 사람이 선택해서 넣어줘야 한다.
* 딥러닝 : 은닉층이 다수 포함된 심층신경망(deep neural network) 형태이다. 한계를 극복하고, 성능이 뛰어나다는 의미 포함. 좋은 특징을 추출하는 것까지 잘 해준다. 특징이 중요하면 알아서 높은 가중치를 넣ㅇ주는 것까지 내제되어 있다. 사람의 편향을 배제하여 오류가 적고, 추론시간이 짧아지며 더 성능이 좋음.


* 딥러닝의 장르 : 이미지 처리, 자연어 철, 음성인식 등에서 급격한 발전. 다만, 딥러닝의 단점으로는 parameter수가 많아서 더 많은 학습 데이터 필요하고, 최적 모델, 훈련을 위한 시간, 비용이 필요하다.
* 기울기 소멸 문제 (Vanishing Gradient Problem) : 난제 중 하나였음. 은닉층 많을수록 더 복잡한 문제를 해결할 수는 있지만, 이게 너무 깊어지면, 역전파를 위해 가중치, bias 변경하는 수학적 방법인 미분이 불가능해져, 0으로 수렴(소멸)되는 문제가 발생한다. 여기서 활성화함수는 가중치를 찾는데 적합한 통계적 함수를 뜻하는데, 효과적인 활성화 함수를 찾는 다양한 연구 진행중이다.
그래서 보통 딥러닝에서는 sigmoid, 쌍곡탄젠트 대신 ReLU를 사용한다.
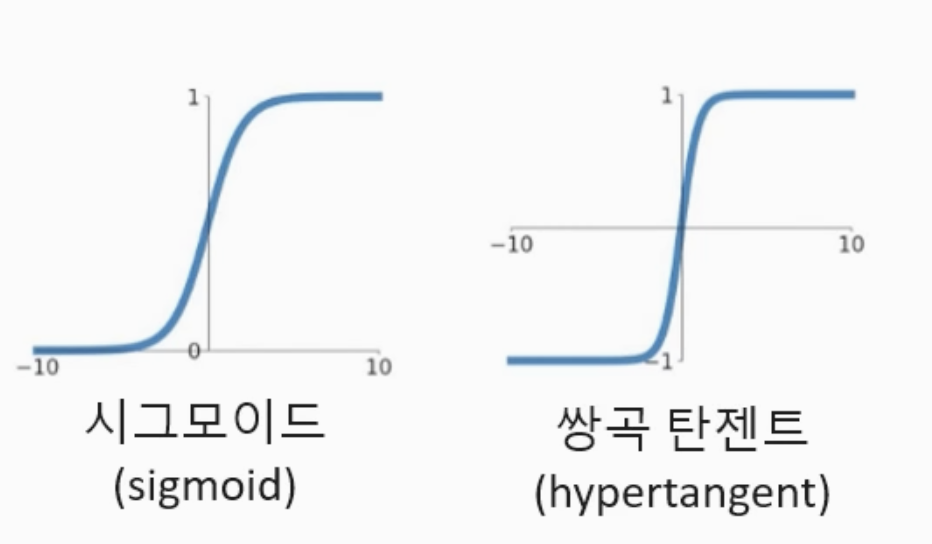
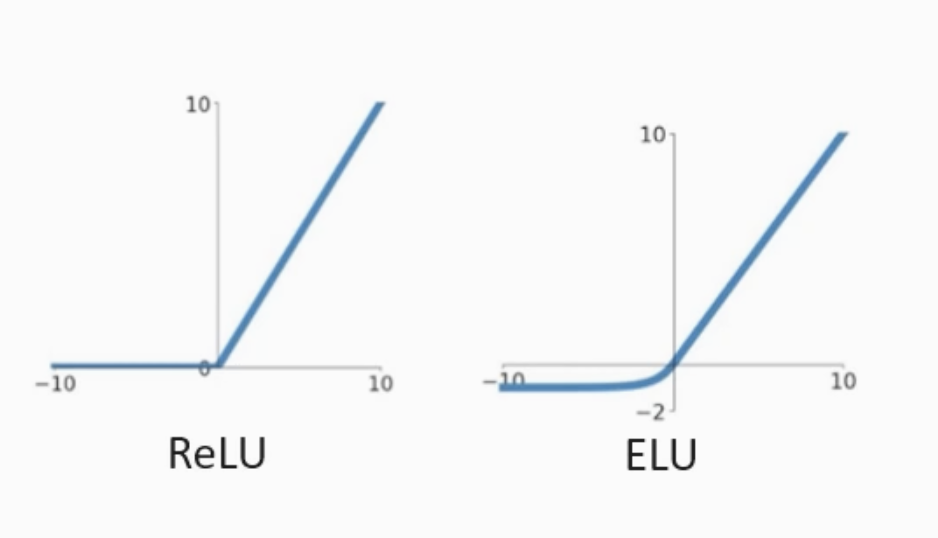
* 과적합(overfitting) : parameter가 너무 많아서 모든 데이터에 지나치게 맞춰진 상태다. 그러면 학습되지 않은 데이터에 대해 성능이 저하될 수 있다. 이를 해결하기 위한 방법들 대표 3가지
- Regularization 규제화 : 큰 가중치에 큰 규제를 가해 과적합되지 않도록 제한. 규제의 강도를 정하는 적절한 가중치를 부여
- Dropout : 노드들을 무작위 선택하여, 연결된 가중치 연결선을 없는 것으로 간주하고 학습 (선택안된 노드들을 없다고 간주)

- Batch Normalization : 모델에 입력되는 샘플을 균일하게 만드는 방법. 미니 배치 단위로 평균 0, 표준편차 1이 되도록 정규화

* 딥러닝의 발전

* 많이 쓰이는 프레임워크

요즘은 딥러닝할때 파이토치를 많이 쓴단다

* 딥러닝의 여러가지 학습 방법

1. 텐서
텐서 : 데이터를 담는 컨테이너라고 본다. (다차원 배영ㄹ, 리스트 형태와 유사). 보통 수치형 데이터 저장하며, 동적 크기를 가짐

-rank : 축의 갯수
-shape : 형상 (축에 따른 차원 개수)
-type : 데이터 타입


2. 텐서의 타입과 변환

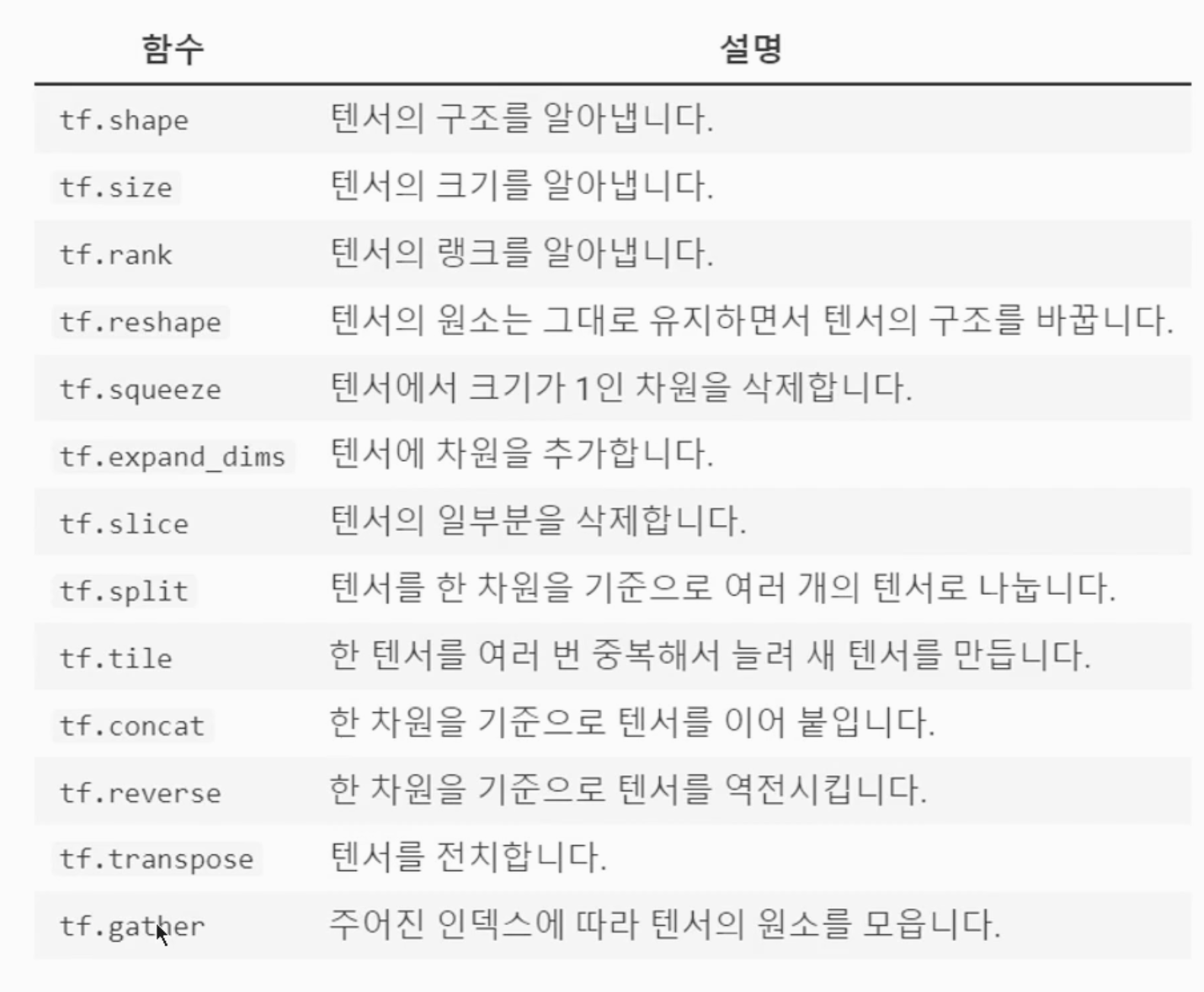
텐서의 타입을 변환하고자 할 때는 tf.cast를 사용합니다.
f32 = tf.cast(f16, tf.float32)
print(f32)- 여기서는 16비트 실수형 tf.float16을 32비트 실수형 tf.float32로 변환하였습니다.
3. 텐서 연산
| + | add() | 더하기 연산 |
| - | subtract() | 빼기 연산 |
| * | multiply() | 곱하기 연산 |
| / | divide() | 나누기 연산 |
| @ | matmul() | 행렬곱 연산 |
| reduce_max() | 텐서 값 중 최대값 | |
| argmax() | 최대값의 위치 반환 | |
| nn.softmax() | 텐서의 값을 0과 1 사이의 값으로 보여줌 |
1. 딥러닝 구조

2. 레이어 (Core layer)
- 딥러닝은 다층 구조, 여러 개의 layer로 구성되어 있다 (input, hidden, output으로 구조되어 있다)
- 레이어는 하나 이상의 텐서를 입력 받아, 하나 이상의 텐서를 출력하는 데이터 처리 모듈인거다
| Input 객체
어떤 입력데이터를 어떤 모양 shape, dtype등으로 받을 것인지를 결정
#Input 객체는 배치 크기를 batch_size로 지정할 수 있고, name을 통해서 이름을 지정할 수도 있습니다.
keras.Input(shape=(28, 28), dtype=tf.float32, batch_size=16, name='input')
| Dense
완전 연결계층(fully-connected layer)
#노드 수(유닛수)를 지정해준다
layers.Dense(10, activation='relu', name='Dense Layer')
| Activation
- 활성화함수는 입력값을 어떤 값으로 변환해 출력할지 결정하는 함수 (sigmoid, relu 등)
- 딥러닝에서는 선형 활성화 함수를 사용하면 다층 구조를 사용하는 의미가 없기 때문에 모델 표현력을 위해서 비선형 활성화 함수 를 사용
- 0, 1에 포화되는 문제가 있기는 하다. 너무 몰리는거지.



- ReLU 가 좋긴 한데, 다만 출력이 다 0으로만 하는 문제가 생길 수 있다. 그래서 그걸 보완한게 Leaky ReLU
| Flatten
batch 크기(데이터 크기)를 제외하고는 데이터를 1차원 형태로 평평하게 변환
inputs = keras.Input(shape=(224, 224, 1))
layer = layers.Flatten()(inputs)
print(layer.shape)
#result
224x224를 한 50176 이 나온다
3. 딥러닝 모델
#모델과 유틸리티를 사용할 수 있도록
from tensorflow.keras import models, utils
| Sequential API
아주 간단한 방법이다. 순차적 구조로 진행할 때만 사용
다중 입력, 다중 출력이 존재할 경우 사용 불가
model = models.Sequential()
model.add(layers.Input(shape=(28, 28)))
model.add(layers.Dense(300, activation='relu'))
model.add(layers.Dense(100, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.summary()
#다른 방법으로 한번에 추가 가능
model = models.Sequential([layers.Input(shape=(28, 28), name='Input'),
layers.Dense(300, activation='relu', name='Dense1'),
layers.Dense(100, activation='relu', name='Dense2'),
layers.Dense(10, activation='softmax', name='Output')])
#plot_model() 함수로 딥러닝 모델을 시각적으로 확인 가능
utils.plot_model(model)model = models.Sequential()
# (100, 100, 3) 형태의 데이터를 받는 Input 레이어를 쌓으세요.
model.add(layers.Input(shape=(100, 100, 3)))
# Flatten 레이어를 쌓으세요.
model.add(layers.Flatten())
# Unit의 수는 400, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
model.add(layers.Dense(400, activation='relu'))
# Unit의 수는 200, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
model.add(layers.Dense(200, activation='relu'))
# Unit의 수는 100, 활성화함수는 Softmax를 사용하는 Dense 레이어를 쌓으세요.
model.add(layers.Dense(100, activation='softmax'))
model.summary()
| Functional API
모델 생성할 때 권장하는 방법. 일반적으로는 이걸 많이 쓴다.
모델을 복잡, 유연하게 구성 가능
다중 입출력을 다룰 수 있음
Functional API를 이용하면 Input 객체를 여러 레이어에서 사용하는 것이 가능합니다.
아래의 예제에서는 Concatenate()를 이용하여 Dense 레이어 결과와 Input을 결합하였습니다.
inputs = layers.Input(shape=(28, 28, 1))
x = layers.Flatten(input_shape=(28, 28, 1))(inputs)
x = layers.Dense(300, activation='relu')(x)
x = layers.Dense(100, activation='relu')(x)
x = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=inputs, outputs=x)
model.summary()
#Dense, Input 레이어를 결합
inputs = keras.Input(shape=(28, 28))
hidden1 = layers.Dense(100, activation='relu')(inputs)
hidden2 = layers.Dense(30, activation='relu')(hidden1)
concat = layers.Concatenate()([inputs, hidden2])
output = layers.Dense(1)(concat)
model = models.Model(inputs=[inputs], outputs=[output])
model.summary()#Input 객체를 여러개 사용하는 것도 가능
input_1 = keras.Input(shape=(10, 10), name='Input_1')
input_2 = keras.Input(shape=(10, 28), name='Input_2')
hidden1 = layers.Dense(100, activation='relu')(input_2)
hidden2 = layers.Dense(10, activation='relu')(hidden1)
concat = layers.Concatenate()([input_1, hidden2])
output = layers.Dense(1, activation='sigmoid', name='output')(concat)
model = models.Model(inputs=[input_1, input_2], outputs=[output])
model.summary()
# (100, 100, 3) 형태의 데이터를 받는 Input 레이어를 쌓으세요
inputs = layers.Input(shape=(100,100,3))
# Flatten 레이어를 쌓으세요.
x = layers.Flatten()(inputs)
# Unit의 수는 400, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
x = layers.Dense(400, activation='relu')(x)
# Unit의 수는 200, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
x = layers.Dense(200, activation='relu')(x)
# Unit의 수는 100, 활성화함수는 Softmax를 사용하는 Dense 레이어를 쌓으세요.
x = layers.Dense(100, activation='softmax')(x)
model = models.Model(inputs = inputs, outputs = x)
model.summary()
| Subclassing API
커스터마이징에 최적화된 방법으로 Model클래스 상속받아 사용
Functional API로 구현 불가한 모델도 구현 가능
객체지향 프로그래밍에 익숙해야함
- fit(): 모델 학습
- evaluate(): 모델 평가
- predict(): 모델 예측
- save(): 모델 저장
- load(): 모델 불러오기
- call(): 메소드안에서 원하는 계산 가능
# Subclassing API의 예시
class MyModel(models.Model):
def __init__(self, units=30, activation='relu', **kwargs):
super(MyModel, self).__init__(**kwargs)
self.dense_layer1 = layers.Dense(300, activation=activation)
self.dense_layer2 = layers.Dense(100, activation=activation)
self.dense_layer3 = layers.Dense(units, activation=activation)
self.output_layer = layers.Dense(10, activation='softmax')
def call(self, inputs):
x = self.dense_layer1(inputs)
x = self.dense_layer2(x)
x = self.dense_layer3(x)
x = self.output_layer(x)
return x
class YourModel(models.Model):
def __init__(self, **kwargs):
super(YourModel, self).__init__(**kwargs)
# Flatten 레이어를 쌓으세요.
self.flat_layer = layers.Flatten()
# Unit의 수는 400, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
self.dense_layer1 = layers.Dense(400, activation='relu')
# Unit의 수는 200, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
self.dense_layer2 = layers.Dense(200, activation='relu')
# Unit의 수는 100, 활성화함수는 Softmax를 사용하는 Dense 레이어를 쌓으세요.
self.output_layer = layers.Dense(100, activation='softmax')
def call(self, inputs):
# Flatten 레이어를 통과한 뒤 Dense 레이어를 400 -> 200 -> 100 순으로 통과하도록 쌓으세요.
x = self.flat_layer(inputs)
x = self.dense_layer1(x)
x = self.dense_layer2(x)
x = self.output_layer(x)
return x
# (100, 100, 3) 형태를 가진 임의의 텐서를 생성해줍니다.
data = tf.random.normal([1, 100, 100, 3])
# 데이터는 일반적으로 batch 단위로 들어가기 때문에 batch 차원을 추가해주겠습니다.
data = tf.reshape(data, (-1, 100, 100, 3))
model = YourModel()
model(data)
model.summary()
1. 손실 함수
-학습이 얼마나 잘 되고 있는지 나타내는 지표 (최소화되어야 하는 값)
-손실함수 결과값에 따라 파라미터를 조정해가면서 학습을 진행한다
-미분 가능한 함수를 사용한다

* Regression에서 많이 사용 : MAE(오차가 매우 크더라도(outlier) 제곱항으로 영향을 미치는 것이 아니라 차이의 절대값만큼만 영향을 미치기 때문에 MSE에 비해 상대적으로 이상치에 더 강건합니다), MSE
* Classification 에서 사용 : Cross entropy error

2. 옵티마이저와 지표
옵티마이저 : 손실함수를 기반으로 모델이 어떻게 업데이트되어야 하는지 결정
- keras.optimizer.SGD() : 기본적 확률적 경사하강법
- keras.optimizer.Adam() : 자주 사용된다
보통, 옵티마이저의 튜닝을 위해 따로 객체를 생성해 컴파일시에 포함한다



안장점에서는 기울기가 0이라서 경사하강법이 이동할 수가 없다. 원래는 그 기울기의 반대방향으로 이동하는 식이니까.


-발산 : 오버슈팅
3. 딥러닝 모델 학습

학습 과정 :
- 먼저 데이터셋을 입력 와 실제 정답(레이블)인 로 구분합니다.
- 입력 데이터는 연속된 레이어로 구성된 네트워크(모델)를 통해 결과로 예측 ′을 출력합니다.
- 손실 함수는 모델이 예측한 ′과 실제 정답인 와 비교하여 얼마나 차이가 나는지 측정하는 손실 값을 계산합니다.
- 옵티마이저는 손실 값을 사용하여 모델의 가중치를 업데이트하는 과정을 수행합니다.
- 모델이 새롭게 예측한 ′과 실제 정답인 의 차이를 측정하는 손실 값을 계산하는 과정을 반복합니다.
- 계산한 손실값을 최소화하도록 옵티마이저가 동작하는 것이 딥러닝 모델 학습입니다.
'Data Scientist Bootcamp' 카테고리의 다른 글
| [3/8] 딥러닝 심화2 (모델의 과소적합, 과대적합을 방지하기 위한 방법 3가지) (0) | 2024.03.08 |
|---|---|
| [3/8] 딥러닝 심화 (학습시킨 모델 저장, 관리/ 모델학습기술 optimizer, activation function 등) (1) | 2024.03.08 |
| [3/6] 인공지능과 가위바위보 하기 (딥러닝) (0) | 2024.03.06 |
| 0304 _ Financial Time series 모델링 (0) | 2024.03.04 |
| [2/27] 시계열 데이터 분석 (Time Series) (1) | 2024.02.27 |




