무냐의 개발일지
ARIMA 모델에서 가장 중요한 정상성 확인 | ADFuller test에 대하여 본문
In ARIMA time series forecasting, the first step is to determine the number of differencing required to make the series stationary.
ARIMA 의 첫 번째 단계는 시계열을 정상적으로 만들기 위해 필요한 차분의 수 !!
Since testing the stationarity of a time series is a frequently performed activity in autoregressive models, the ADF test along with KPSS test is something that you need to be fluent in when performing time series analysis.
그래서 시계열의 정상성을 파악하기 위해 ADF, KPSS 는 매우 중요하고, 잘 익혀야한다
Another point to remember is the ADF test is fundamentally a statistical significance test. That means, there is a hypothesis testing involved with a null and alternate hypothesis and as a result a test statistic is computed and p-values get reported.
The ADF test belongs to a category of tests called ‘Unit Root Test’, which is the proper method for testing the stationarity of a time series. So what does a ‘Unit Root’ mean?
ADF 는 단위근 테스트의 범주에 속한다.
Unit root is a characteristic of a time series that makes it non-stationary. Technically speaking, a unit root is said to exist in a time series of the value of alpha = 1 in the below equation.
단위근은 시계열을 비정상으로 만드는 특징이다. 아래 식에서 알파 =1 인 경우, 단위근이 존재한다.
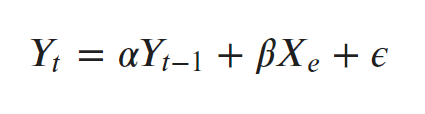
where, Yt is the value of the time series at time ‘t’ and Xe is an exogenous variable (외생변수 : a separate explanatory variable, which is also a time series).
What does this mean to us?
The presence of a unit root means the time series is non-stationary. Besides, the number of unit roots contained in the series corresponds to the number of differencing operations required to make the series stationary.
단위근이 존재한다는 건, 시계열이 비정상이라는 거다. 그리고, 데이터에 포함된 단위근의 갯수 = 데이터를 정상으로 만들기 위해 필요한 차분의 연산 수
A Dickey-Fuller test is a unit root test that tests the null hypothesis that α=1 in the following model equation. alpha is the coefficient of the first lag on Y.
ADF의 귀무가설은 알파 = 1 이다. (시계열은 비정상적이다)
Null Hypothesis (H0): alpha=1
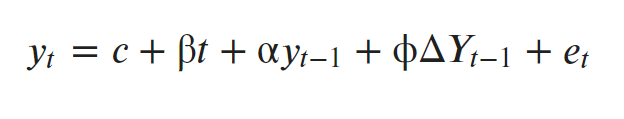
where,
- y(t-1) = lag 1 of time series
- delta Y(t-1) = first difference of the series at time (t-1)
Fundamentally, it has a similar null hypothesis as the unit root test. That is, the coefficient of Y(t-1) is 1, implying the presence of a unit root. If not rejected, the series is taken to be non-stationary.
The Augmented Dickey-Fuller test evolved based on the above equation and is one of the most common form of Unit Root test.
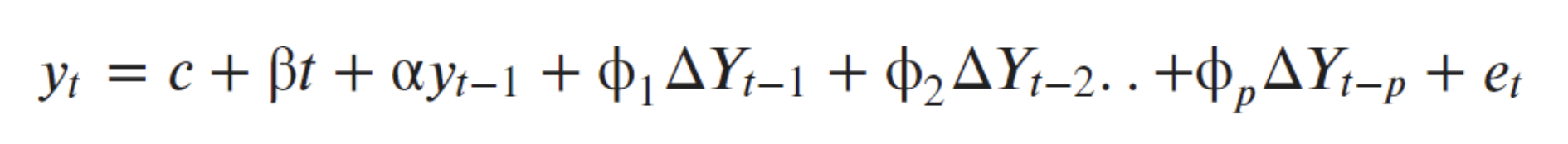
The ADF test expands the Dickey-Fuller test equation to include high order regressive process in the model.
기존 DF 테스트에 뒤에 추가적으로 2차분... p차분까지 더한게 ADF이다.
If you notice, we have only added more differencing terms, while the rest of the equation remains the same. This adds more thoroughness to the test. The null hypothesis however is still the same as the Dickey Fuller test.
A key point to remember here is: Since the null hypothesis assumes the presence of unit root, that is α=1, the p-value obtained should be less than the significance level (say 0.05) in order to reject the null hypothesis. Thereby, inferring that the series is stationary.
However, this is a very common mistake analysts commit with this test. That is, if the p-value is less than significance level, people mistakenly take the series to be non-stationary. (헷갈리지 말자! ADF에서는 귀무가설이, 시계열이 안정적이지 않다 이다)
아래 네가지 값을 내는데,
- The p-value
- The value of the test statistic
- Number of lags considered for the test
- The critical value cutoffs.
When the test statistic is lower than the critical value shown, you reject the null hypothesis and infer that the time series is stationary.
- test statistics < critical value 일 때, 귀무가설을 기각한다
- p-value < 0.05 일 때, 귀무가설을 기각한다
# ADF Test
result = adfuller(series, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'n_lags: {result[1]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
print('Critial Values:')
print(f' {key}, {value}')
# Results
ADF Statistic: 3.1451856893067296
n_lags: 1.0
p-value: 1.0
Critial Values:
1%, -3.465620397124192
Critial Values:
5%, -2.8770397560752436
Critial Values:
10%, -2.5750324547306476
여기서 statistics > critical value 니까,
그리고 p-value > 0.05 니까, 귀무가설을 기각하지 않는다!!!
(참고)
'데싸 추가 독학' 카테고리의 다른 글
| [자료구조] 파이썬으로 계산기 만들기 (Stack) (0) | 2024.04.09 |
|---|---|
| 파이썬 클래스, 객체, 계좌만들기 실습 (0) | 2024.04.08 |
| [머신러닝] 머신러닝에 사용되는 라이브러리 순서!! (0) | 2024.02.19 |
| [데이터 과학을 위한 통계]#1 EDA 탐색적 데이터분석 (0) | 2024.02.18 |
| [Python] Heatmap으로 그래프 그리기 (0) | 2024.02.13 |


